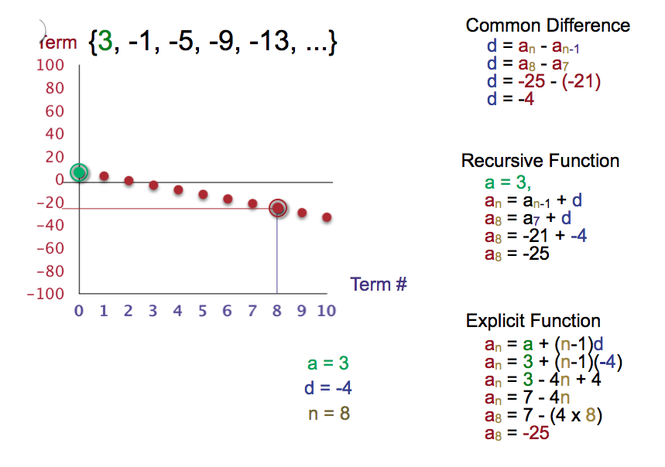
PowerPoint to teach Arithmetic Sequences - Multiple Representations
This PowerPoint was originally written to work with applets through a complex website; however, there is a lot of value in simply providing it for teachers. So much work went into this, and I am pleased if it can be useful to you.
The colours are consistent throughout, and there is a clear relationship between patterns of tiles, arithmetic sequences, and linear relationships. Also, multiple ways of representing are used, including numerical sequences, tables, graphs, and formulas. Implementation: I recommend that you distribute colour tiles (or square crackers!) and have the students build the first three piles of tiles as shown on the fourth PowerPoint slide. Then, they can guess what the next pile looks like. Ask them how they saw the piles changing. You will see that students describe differently how they visualized the piles growing. Discussing students' interpretations is important. Then ask them to make a table of values and look for patterns as you develop the formulas together :) | |||